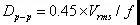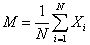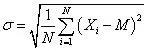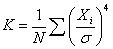来源：摘录自百度文库《附录5 机器振动监测和分析》

各种机器的振动信号成分可以简单地分为三类：正弦振动，随机振动及冲击振动。

习惯上，位移振幅单位为μm，采用峰峰值；速度振幅单位为mm/s，采用有效值；加速度振幅单位mm/s²或g，采用峰值。但也不尽然，例如，著名的GE公司对燃气轮机出厂试验的标准却是以轴承座上速度值的峰值为依据的。

因为振动位移比较直观，人们往往在测量出速度振幅后还希望折算到振动位移值，它们之间的一个简单的换算方法是：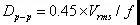

式中，Dp-p 是位移的峰峰值，Vrms 是速度幅值的均方根值，f  是正弦振动的频率 (Hz)。例如，振动速度的均方根值等于1mm/s，则对应的位移峰峰值等于4.5μm。

实际机器的振动绝不可能是单一频率的正弦振动。这种情况下，振动的峰值或峰峰值变得十分复杂，往往在某一个相等的短时间间隔内，它们不是一个常值，有时甚至变化很大。上式换算出来的位移振幅只是一个当量值，并不真实代表振动位移的最大值。有的机组出厂标准采用位移的真峰峰值，这种情况下，振动读数会比按上式的标准高得多。

2. 频率是分析振动原因的主要依据。

不同的振源引起不同频率的振动，这也是为什么频率分析是振动故障分析的主要方法受到特别重视的原因。对于旋转机械的振动，根据振动频率分为同步振动和非同步振动。同步振动的频率是机器运行转速的整倍数或分数，典型的同步振动有1X，2X，1/2X以及0.43X。

3. 相角实际机器振动十分复杂，讨论机器上某一点振动的相角是没有意义的。

只有单一频率纯正弦振动才有相角的概念。例如，轴振动的工频分量（与转速对应的频率）与轴上某一固定标志的相位差，转子“高点”就是基于相角测量。所谓“高点”是轴上的某一点（方向），当该点转到径向振动位移传感器的位置时，振动正好是正峰值。通过确定转子上高点的位置，能确定转子平衡状态及残余不平衡量的位置。

4. 机器振型十分复杂，即使稳定振动，其振型也是瞬时变化的。

模态分析经过参数识别获得的是机器的固有振型。实际机器承受一个或多个激励频率，是一个或多个强迫振动以及随机噪声的迭加。转轴振型则有实际意义，在一定转速下，转轴沿轴向的振动变形就是转子振型。对于单个转子而言，经过某一阶临界转速，振型发生变化；对于多跨转子，每隔一定距离放置一组互相垂直的径向位移传感器，并利用基准相位信息就可以获得转子沿轴向的振动形状，它有助于估计转子与固定部件之间的间隙以及节点位置。

均值：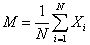

均方根值：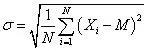

峭度 (Kurtosis)：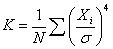

典型信号的峭度系数如下表：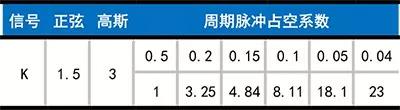

表中，d 为脉冲的占空系数，即脉冲的宽度与重复周期之比。一般运转平衡、无明显周期干扰的，其振动信号的幅值概率密度函数接近于正态分布。因此，峭度系数应为3左右，和振动强弱无关。